1 INTRODUCCIÓN
Esta entrada en el blog continúa con ejercicios sobre series relacionadas con los recíprocos de números especiales, siguiendo trabajos previos1 sobre los números piramidales cuadrados y los números poligonales. En esta ocasión consideramos un ejemplo sencillo: la suma de los recíprocos de los números tetraédricos.
Aunque el resultado no es particularmente profundo, sirve como una buena ilustración del uso de fracciones parciales y series telescópicas.
2 NÚMEROS TETRAÉDRICOS
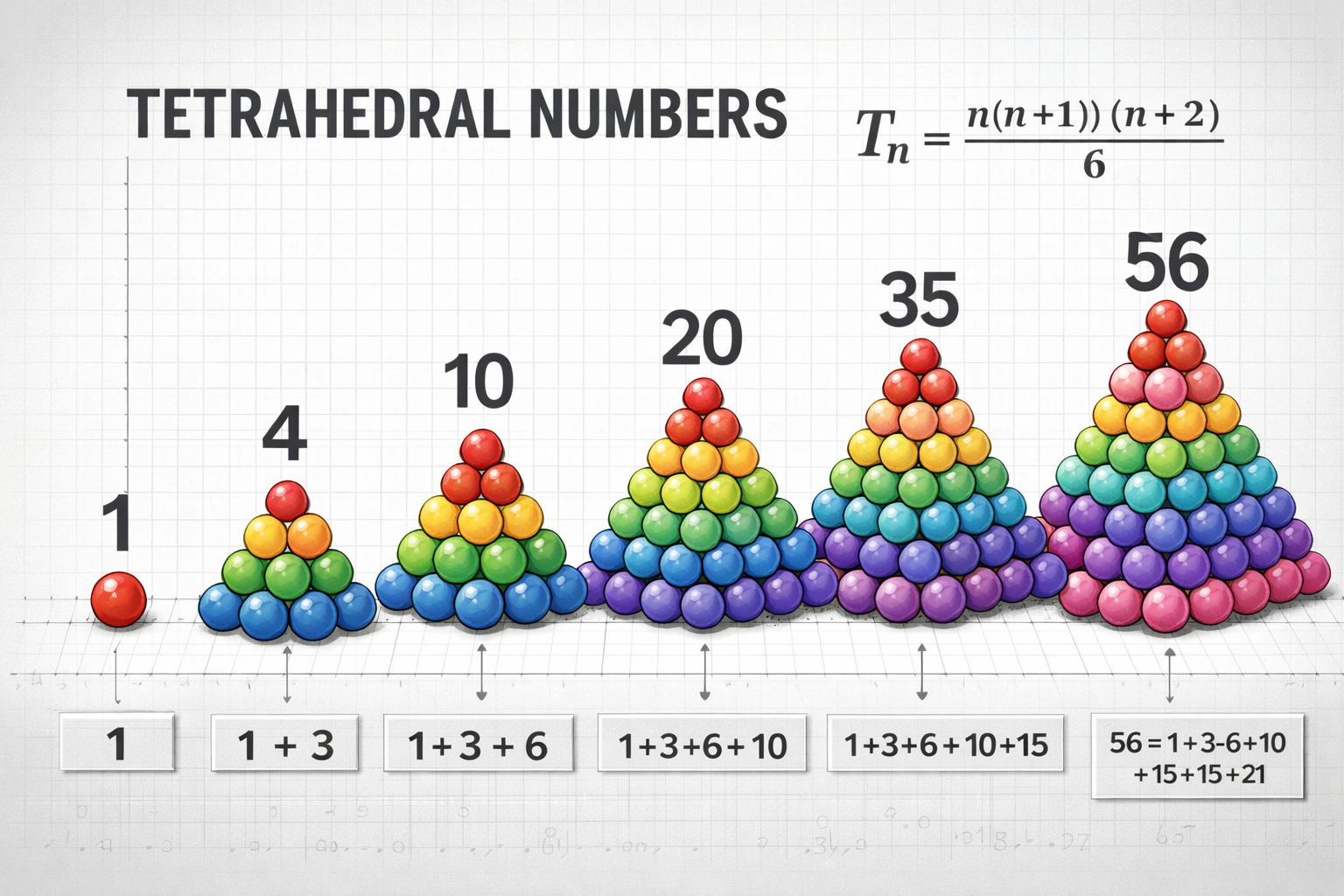
Los números tetraédricos representan el número de esferas que pueden apilarse formando un tetraedro regular [2] [3] y están definidos por la fórmula
T_n = \frac{n(n+1)(n+2)}{6} = \binom{n+2}{3} \tag{1}
3 LA SERIE DE LOS RECÍPROCOS DE NÚMEROS TETRAÉDRICOS
Nos interesa estudiar la suma parcial
S(n) = \sum_{k=1}^{n} \frac{1}{T_k} = \sum_{k=1}^{n} {\binom{k+2}{3}}^{-1} \tag{2}
Sustituyendo la expresión explícita de T_k, obtenemos
S(n) = \sum_{k=1}^{n} \frac{6}{k(k+1)(k+2)} \tag{3}
4 DESCOMPOSICIÓN EN FRACCIONES PARCIALES
La fracción racional (3) puede descomponerse en una suma de otras como:
\frac{6}{k(k+1)(k+2)} = \frac{A}{k} + \frac{B}{k+1} + \frac{C}{k+2} \tag{4}
Resolviendo el sistema lineal correspondiente se obtienen los valores de los denominadores de la descomposición en fracciones parciales:
A = \frac{1}{2}, \qquad B = -1, \qquad C = \frac{1}{2} \tag{5}
Por lo tanto,
\frac{6}{k(k+1)(k+2)} = \frac{1}{2k} - \frac{1}{k+1} + \frac{1}{2(k+2)} \tag{6}
5 NÚMEROS ARMÓNICOS
Estas tres series se pueden sumar facilmente teniendo en cuenta las siguientes identidades para los números armónicos H_n [4]:
\sum_{k=1}^{n} \frac{1}{k} = H_n \tag{7}
\sum_{k=1}^{n} \frac{1}{k+1} = H_n - 1 + \frac{1}{n+1} \tag{8}
\sum_{k=1}^{n} \frac{1}{k+2} = H_n - \frac{3}{2} + \frac{1}{n+1} + \frac{1}{n+2} \tag{9} Sustituyendo estas expresiones en la identidad (6), se obtiene
\begin{align} \frac{S(n)}{6} = \frac{n}{n+1} - \frac{1}{2} - \frac{1}{4} + \frac{1}{2(n+1)} + \frac{1}{2(n+2)} \end{align} \tag{10}
Aquí se observa claramente el carácter telescópico de la serie: los términos H_n se cancelan, evitando la aparición de la constante de Euler-Mascheroni (\gamma) o la función digamma (\psi) partiendo de la extensión clásica de los números armónicos.
H_{n} = \gamma + \psi(n+1) \tag{11}
6 FÓRMULA CERRADA
Simplificando (10), se obtiene una expresión cerrada para la suma parcial:
S(n) = \frac{3n(n+3)}{2(n+1)(n+2)} \tag{12}
Los numeradores y denominadores de (12) son respectivamente las secuencias designadas como A118391 y A118392 en OEIS.
7 SUMA INFINITA
Finalmente, tomando el límite de (12) cuando n \to \infty,
\lim_{n \to \infty} S(n) = \frac{3}{2} \tag{13}
Esto muestra que la serie de los recíprocos de los números tetraédricos converge, y su suma infinita es igual a \frac{3}{2}.